Bài 5 – 6 – 7:

KHÁI NIỆM HÀM SỐ

MẶT PHẰNG TỌA ĐỘ

HÀM SỐ y = ax (a ≠ 0)

–o0o–

Nếu một đại lượng y phụ thuộc vào một đại lượng thay đổi x sao cho một giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, và x gọi là biến số.

1. Hàm số được cho bằng hai dạng : bảng và công thức.

a. Hàm số dạng bảng :

x	0	1	2	3	4	5
y	1	3	5	7	9	11

b. Hàm số bằng công thức (dạng tường minh):

y = f(x)

f(x) là biểu thức đại số với biến x.

Ví dụ :

y = 2 : hàm hằng.

y = 2x +1: hàm số bậc nhất

y = x² +2x -1: hàm số bậc 2

$y=\frac{2x+1}{x-1}$ hàm số nhất biến .v .v …

3. Đồ thị của hàm số :

3.a. Định nghĩa :

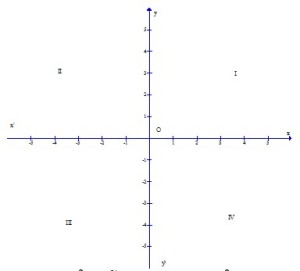
Đồ thị của hàm số y = f(x) là tập hợp các cặp giá trị tương ứng (x ; f(x)) trên mặt phẳng tọa độ.

b. mặt phẳng tọa độ Oxy :

* Ox :trục hoành.

* Oy : trục tung.

* O : gốc tọa độ.

* ( I) góc phần tư thứ I, (II) góc phần tư thứ iI,( III) góc phần tư thứ III,( IV) góc phần tư thứ IV.

c. Biểu diễn tọa độ một điểm A trên mặt phẳng tọa độ Oxy:

Ta có : A(x_A; y_A) trong đó : x_A: hoành độ của điểm A .

y_A: hoành độ của điểm A .

ví dụ Biểu diễn tọa độ một điểm A(2 ; 3)

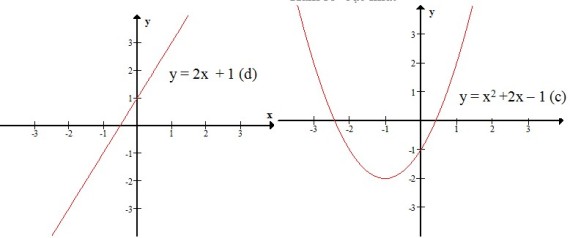
vẽ đồ thị của một hàm số trên mặt phẳng tọa độ:

y = x² +2x – 1 (c); y = 2x + 1 (d)

4. Vị trí tương đối giữa điểm và đồ thị hàm số :

cho A(x_A; y_A) và hàm số y = f(x) có đồ thị (c). A thuộc (c) khi y_A = f(x_A)

ví dụ : A(1 ; 2) và B( -2 ; 1) có thuộc y = f(x) = x² +2x – 1 (c)

giải.

Tính : f(x_A) = f(1) = 1² +2.1 – 1 = 2 = y_A

=> A € ( c).

f(x_B) = f(-2) = (-2)² +2.(-2) – 1 = 2 = -1 ≠ y_B

=> B không nằm trên (C).

Đồ thị của hàm số y = ax :

Đồ thị của hàm số y = ax là đường thẳng đi qua gốc tọa độ.