Định lí vi-ét và ứng dụng

Định lí viet thuận :

Nếu phương trình bậc hai có dạng : ax² + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt x₁, x₂ thì

$x_1+x_2=\frac{-b}{a}$

$x_1.x_2=\frac{c}{a}$

Định lí viet đảo :

Nếu ta có hai số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình :

X² – SX + P = 0

=================================

Bài 1 : Cho phương trình: x² + mx + 2m – 4 = 0 (1) (x là ẩn số)

a) Chứng minh phương trình (1) luôn luôn có nghiệm với mọi giá trị của m

b) Tìm m để phương trình có hai nghiệm thỏa: $x_1^2+x_2^2=4$

Δ = b² – 4ac = m² – 4.1.( 2m – 4) = m² – 8m + 16

= m² – 2.4.m + 4² = (m – 4)² ≥ 0 với mọi m.

=> Δ≥ 0 với mọi m.

=> phương trình (1) luôn luôn có nghiệm với mọi giá trị của m

b) theo định lí viet :

$x_1+x_2=\frac{-b}{a}=-m$

$x_1.x_2=\frac{c}{a}=2m-4$

Theo đề bài :

$x_1^2+x_2^2=4$

<=> $(x_1+x_2)^2-2 x_1.x_2=4$

=> $m^2-2(2m-4)=4$

<=> $m^2-4m+4=0$

<=> $(m-2)^2=0$

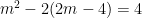
<=> m – 2 = 0

<=> m = 2

Vậy : m = 2.