Blog Toán Học

Bài 15+16+17

Phân tích một số thừa số nguyên tố

ƯỚC CHUNG – BÔI CHUNG

ƯỚC CHUNG LỚN NHẤT– BỘI CHUNG NHỎ NHẤT

–o0o–

1. Phân tích một số ra thừa số nguyên tố :

Phân tích một số tự nhiên lớn 1 ra thừa số nguyên tố là viết số đó dưới dạng tích các thừa số nguyên tố.

Ví dụ :

4 = 2 . 2 = 2²

6 = 2 . 3

8 = 2. 2. 2 = 2³

9 = 3.3 = 3²

12 = 2.2.4 = 2².3

…

Cách phân tích :

Lấy số tự nhiên cần phân tích chia hết số nguyên tố có thể (chọn từ nhỏ đến lớn) bằng dấu hiệu chia hết.

60	2
30	2
15	3
5	5
1

Vậy : 60 = 2.2.3.5 = 2².3.5

2. ƯỚC CHUNG :

Ước chung của hai hay nhiều số là ước của tất cả các số đó.

Kí hiệu :

ƯC(a, b) : Ước chung của hai số a và b.

Ta có : x 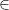$\in$ ƯC(a, b) nếu a $\vdots$ x và b $\vdots$ x.

ƯC(a, b, c) : Ước chung của hai số a và b, c.

Ta có : x 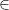$\in$ ƯC(a, ,b, c) nếu a $\vdots$ x và b $\vdots$ x và c $\vdots$ x

Cách tìm :

ƯC(a, b) = Ư(a) ∩ Ư(b)

ƯC(a, b, c) = Ư(a) ∩ Ư(b) ∩ Ư(c)

3. BỘI CHUNG :

Bội chung của hai hay nhiều số là bội của tất cả các số đó.

Kí hiệu :

BC(a, b) : bội chung của hai số a và b.

Ta có : x 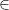$\in$ BC(a, b) nếu x $\vdots$ a và x $\vdots$ b.

ƯC(a, b, c) : Ước chung của hai số a và b, c.

Ta có : x 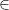$\in$ Ư(a, ,b, c) nếu x $\vdots$ a và x $\vdots$ b và x $\vdots$ c

Cách tìm :

BC(a, b) = B(a) ∩ B(b)

BC(a, b, c) = B(a) ∩ B(b) ∩ B(c)

4. ƯỚC CHUNG LỚN NHẤT :

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Cách tìm Ước chung lớn nhất :

Phân tích một số ra thừa số nguyên tố.

Chọn ra thừa số nguyên tố chung.

Lập tích các thừa số đã chọn. mỗi thừa số lấy số mũ nhỏ nhất. tích đó là ƯCLN phải tìm.

Ví dụ :

ƯCLN(12, 30)

Ta có :

12 = 2.2.3 = 2².3

30 = 2.3.5

ƯCLN(12, 30) = 2.3 = 6

ƯCLN(24, 16, 8)

Ta có :

24 = 2.2.2.3 = 2³.3

16 = 2.2.2.2 = 2⁴

8 = 2.2.2 = 2³

ƯCLN(24, 16, 8) = 2³ = 8

Tìm ước chung :

ƯC(a, b) = Ư(ƯCLN(a, b))

ƯC(12, 30) = Ư (6) = {1, 2, 3, 6}

5. BỘI CHUNG NHỎ NHẤT BCNN:

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Cách tìm bội chung nhỏ nhất :

Phân tích một số ra thừa số nguyên tố.
Chọn ra thừa số nguyên tố chung và riêng.
Lập tích các thừa số đã chọn. mỗi thừa số lấy số mũ lớn nhất. tích đó là BCNN phải tìm.

Ví dụ :

BCNN(8, 12)

Ta có :

8 = 2.2.2 = 2³

12 = 2.2.3 = 2².3

BCNN(8, 12) = 2³.3 = 8.4 = 24

BCNN(12, 16, 48)

12 = 2.2.3 = 2².3

16 = 2⁴

48 = 2⁴.3

BCNN(12, 16, 48) = 2⁴.3 = 48

Tìm BC :

BC(a, b) =B(BCNN(a, b))

ví dụ :tìm BC(12, 16, 48)

Theo ví dụ trên ta có : BCNN(12, 16, 48) = 2⁴.3 = 48

vậy : BC(12, 16, 48) = B(48) = {48, 96, 144, …}