Bài 2

Căn thức bậc hai và hằng đẳng thức

–o0o-–

1. Căn thức bậc hai :

Với A là một biểu thức đại số,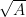\sqrt{A}  người ta gọi là Căn thức bậc hai của A, còn A được gọi là  biểu thức lấy căn hay biểu thức dưới căn.

2. Điều kiện xác định (có nghĩa) của Căn thức bậc hai :

\sqrt{A} xác định khi  : A ≥ 0

3. hằng đẳng thức :

với mọi số A, ta có :\sqrt{A^2}=|A|

4. bài tập

====

1. Dạng tìm điều kiện Căn thức bậc hai có nghĩa : 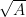\sqrt{A} xác định khi  : A ≥ 0

Bài 6d/T10 \sqrt{2a+7}
có nghĩa khi : 2a + 7 ≥ 0 <=> a ≥ -7/2
Bài 12c/ t11 : \sqrt{\frac{1}{-1+x}}
có nghĩa khi :  \frac{1}{-1+x} ≥ 0 và -1 + x ≠ 0 <=> -1 + x > 0 <=> x > 1
===============

2. Dạng tính và rút gọn sữ dụng :\sqrt{A^2}=|A|  và |A| = A (A ≥ 0 ) hoặc -A (A <0)

Bài 7/T10 : 

a.  \sqrt{(0,1)^2} =|0,1|=0,1
b.  \sqrt{(-0,3)^2} =|-0,3|=0,3
c.  -\sqrt{(-1,3)^2} =-|-1,3|=-1,3
Bài 8/T10 : 
a.  \sqrt{(2-\sqrt{3})^2} =|2-\sqrt{3}|=2-\sqrt{3}(2-\sqrt{3}>0)
b.  \sqrt{(3-\sqrt{11})^2} =|3-\sqrt{11}|=-(3-\sqrt{11})=\sqrt{11}-3(3-\sqrt{11}<0)
c.  2\sqrt{a^2} =2|a|=2a  (vì a ≥ 0)
d.  3\sqrt{(a-2)^2} =3|a-2|=6-3a  vì  a < 2 ; -(A – B) = B – A
Bài 13 /t11
a.  2\sqrt{a^2}-5a =2|a|-5a=-2a-5a=-7a  (vì a < 0)
b.  \sqrt{25a^2}+3a =|5a|+3a=5a+3a=8a  (vì a ≥ 0)
bài 9 /t11 : tìm x :
a.  \sqrt{x^2} =7
<=> |x| = 7  <=> x = 7  hoặc  x = -7
===============

Bài tập bổ sung :

1. Dạng giải phương trình căn :

bài 1 : 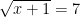\sqrt{x+1}=7
<=> x +1  = 49 (vì 7 > 0)
<=> x = 48
Bài 2 : \sqrt{x^2+3x-4}=x-1  (2)
Khi x – 1 ≥ 0 <=> x ≥ 1
(2) <=> x2  + 3x – 4 = (x  – 1 )2 = x2 -2x + 1
 <=> 3x – 4 = -2x + 1
<=> x = 1  ( nhận)
vậy : S = { 1}.
Bài 3 : \sqrt{x^2-4x+4} =7-x
<=> \sqrt{(x-2x)^2} =7-x
<=> |x – 2| =7-x (3)
Nếu x – 2 ≥ 0 <=> x ≥ 2 thì :
(3) trở thành : x – 2 = 7 – x <=> x = 9/2 ≥ 2 (nhận).
Nếu x – 2 < 0 <=> x < 2 thì :
(3) trở thành : -(x – 2) = 7 – x <=> 0.x = 5 vô nghiệm mọi x
Vậy : S = {9/2 }.
===============

3.Dạng căn chứa căn :

Bài 1 : tính  \sqrt{4-2\sqrt{3}}
Ta có :  \sqrt{4-2\sqrt{3}} =\sqrt{3-2.\sqrt{3}.1+1}=\sqrt{(\sqrt{3})^2-2.\sqrt{3}.1+1^2}
=\sqrt{(\sqrt{3}-1)^2} =|\sqrt{3}-1|=\sqrt{3}-1(\sqrt{3}-1>0)
bài 2 : tính A=4+\sqrt{(2+\sqrt{3})^2}+\sqrt{4+2\sqrt{3}}
Ta có : A=4+\sqrt{(2+\sqrt{3})^2}+\sqrt{4+2\sqrt{3}}=4+|2+\sqrt{3}|+\sqrt{(\sqrt{3}+1)^2}
=6+\sqrt{3}+|\sqrt{3}+1|=7+2\sqrt{3}

phương pháp giải :

Bước 1 : biến đổi biểu thức trong căn về dạng : (…)2 .
(A  ± B )2 = A2 ± 2AB + B2
Bước 2 : Dùng công thức : \sqrt{A^2}=|A|