BÀI 2 – 3 – 4

Hệ phương trình bậc nhất hai ẩn – cách giải

–o0o–

Định nghĩa :
Hệ phương trình bậc nhất hai ẩn có dạng : \begin{cases}ax+by=c(1) \\ a'x+b'y=c' (2)\end{cases}
Giải hệ phương trình bằng phương pháp thế :
Bước 1 : chọn một phương trình biểu diễn nghiệm đơn gian nhất.
Bước 2 : thế vào phương trình còn lại.
Giải hệ phương trình bằng phương pháp đại số :
Bước 1 : cộng hay trừ từng vế hai phương trình của hệ phương trình cho ra phương trình mới.
 Bước 2 : dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia).
Ví dụ : giải hệ phương trình :
\begin{cases}4x+3y=6(1) \\ 2x+y=4 (2)\end{cases}(*)
Giải.
Giải hệ phương trình bằng phương pháp thế :
Ta nhận thấy với Phương trình (2) biểu diễn nghiệm đơn giản nhất.
\Leftrightarrow\begin{cases}4x+3y=6(1) \\ 2x+y=4 (2)\end{cases}\\ \Leftrightarrow\begin{cases}4x+3y=6 \\ y=4 -2x \end{cases}\\ \Leftrightarrow\begin{cases}4x+3y=6 \\ y=4 -2x \end{cases}\\ \Leftrightarrow\begin{cases}4x+3(4 -2x)=6 \\ y=4 -2x \end{cases}\\ \Leftrightarrow\begin{cases}x=3 \\ y=-2 \end{cases}
Giải hệ phương trình bằng phương pháp đại số :
Ta nhận thấy rằng khử biến x bằng cách : nhân -2 vào hai vế phương trình (2), sau đó cộng từng vế của hai phương trình.
\Leftrightarrow\begin{cases}4x+3y=6(1) \\ 2x+y=4 (2)\end{cases}\\ \Leftrightarrow\begin{cases}4x+3y=6\\ -4x-2y=-8 [(2).(-2)]\end{cases}\\ \Leftrightarrow\begin{cases}4x+3y=6\\ y=-2 \end{cases}\\ \Leftrightarrow\begin{cases}x=3\\ y=-2 \end{cases}

========================

BÀI TẬP SGK :

BÀI 12 TRANG 15 : giải các hệ phương trình bằng phương pháp thế.
a) 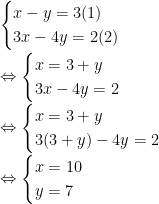     \begin{cases}x-y=3(1) \\ 3x-4y=2 (2)\end{cases}\\ \Leftrightarrow\begin{cases} x =3+y\\ 3x-4y=2 \end{cases}\\ \Leftrightarrow\begin{cases} x =3+y \\ 3(3+y)-4y=2 \end{cases}\\ \Leftrightarrow\begin{cases}x=10\\ y=7 \end{cases}
vậy : nghiệm của hệ : (10; 7).
————————————————————————————————-
BÀI 20 TRANG 19 : giải các hệ phương trình bằng phương pháp đại số.
a) \begin{cases}3x+y=3(1) \\ 2x-y=7 (2)\end{cases}\\ \Leftrightarrow\begin{cases}3x+y=3\\ 3x+2x=3+7\end{cases}\\ \Leftrightarrow\begin{cases}3x+y=3\\ x=2 \end{cases}\\ \Leftrightarrow\begin{cases}x=2\\ y=-3 \end{cases}
vậy : nghiệm của hệ : (2; -3).