BÀI 5 – 6

GIẢI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH

–o0o–

Phương pháp :
Bước 1 : đặt ẩn và điều kiện cho ẩn.
Bước 2 : thiết lập các phương trình, bằng các mối liên hệ của đề bài.
Bước 3 : giải hệ.
Bước 4 : so điều kiện, chọn kết quả.
Lưu ý : phân tích bài toán bằng bảng phân tích gồm các dòng là các đối tượng và các cột là các đặc điểm của mỗi đối tượng.
đặc điểm 1 đặc điểm 2đặc điểm 3…
đối tượng I
đối tượng II

=========================================================

BÀI TẬP SGK :

BÀI 28 TRANG 22 :
tìm hai số tự nhiên, biết tổng của chúng bằng 1006 và lấy số lớn chia số nhỏ thì được thương là 2 và số dư 124
Giải.
Gọi x là số lớn và y là số nhỏ. Điều kiện : x, y 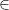\in  N, x > y.
Tổng hai số : x + y = 1006
Phép chia có dư : x = 2y +124 <=> x – 2y = 124
Ta có hệ phương trình :
\Leftrightarrow\begin{cases}x+y=1006(1) \\ x-2y=124 (2)\end{cases}\\ \Leftrightarrow\begin{cases} x+y=1006\\ 3y=1006-124=882 (2) \end{cases}\\ \Leftrightarrow\begin{cases} x+y=1006\\ y=294 \end{cases}\\ \Leftrightarrow\begin{cases}x=712\\ y=294 \end{cases}
Vậy : số lớn là 712 và số nhỏ là 294.
————————————————————————————————-
BÀI 29 TRANG 22 :
Số quảSố phần chia
CamX10x
quíty3y
Tổng17100
GIẢI.
Gọi x, y là số quả cam và quýt. x, y 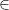\in  N*
Tổng số quả  cam và quýt : x + y = 17
Số phần chia cho 100 người : 10x + 3y = 100
Ta có hệ phương trình :
\Leftrightarrow\begin{cases}x+y=17 \\ 10x+3y=100\end{cases}\\ \Leftrightarrow\begin{cases} x+y=17\\ 7x=100-3.17=49 \end{cases}\\ \Leftrightarrow\begin{cases} x+y=17\\ x=7 \end{cases}\\ \Leftrightarrow\begin{cases}x=7\\ y=10 \end{cases}
Vậy : 7 quả cam và 10 quả quýt.

Bài toán dạng chuyển động :

BÀI 30 TRANG 22 :
bảng phân tích :
Vận tốc (km/h)Quãng đường (km)Thời gian
Dự địnhAB  = st
Thực hiện35st + 2
50st – 1

Giải.

Gọi Quãng đường AB : s (km) s > 0.
Thời gian dự định đi hết Quãng đường AB : t (giờ)  t > 0.
Khi Ôtô chạy Vận tốc 35 (km/h) đến B mất t + 2 giờ : s = 35(t + 2) <=> s – 35t = 70 (1)
Khi Ôtô chạy Vận tốc 50 (km/h) đến B mất t  – 1 giờ : s = 50(t – 1) <=> s – 50t = -50 (2)
Ta có hệ phương trình :
\Leftrightarrow\begin{cases}s-35t=70 \\ s-50t=-50\end{cases}\\ \Leftrightarrow\begin{cases} s-35t=70\\ 15t=70+50=120 \end{cases}\\ \Leftrightarrow\begin{cases} s-35t=70\\ t=8 \end{cases}\\ \Leftrightarrow\begin{cases}s=350\\ t=8 \end{cases}
Vậy : Quãng đường AB là 350 km. thời điểm xuất phát : 12 – 8 = 4 giờ.
———————————————————————————————————

DẠNG TOÁN NĂNG SUẤT :

BÀI 32 TRANG 23 :
BẢNG PHÂN TÍCH :
Thời gian chảy đầy bểNăng suấtPhần bể Thực hiện
VÒI 1x1/x(9+5/6).1/x
VÒI 2y1/y6/5
GIẢI.
Gọi x (giờ) thời gian vòi 1 chảy một mình đầy bể (x > 0).
y (giờ) thời gian vòi 2 chảy một mình đầy bể (y > 0).
Năng suất của vòi 1: 1/x.
Năng suất của vòi 2: 1/y.
Năng suất chung : 1/x + 1/y =5/24 (1)
Thòi gian vòi 1 chảy : 9 + 6/5 = 51/5 (giờ).
Thòi gian vòi 5 chảy : 6/5  (giờ).
Ta được : \frac{51}{5x} +\frac{6}{5y} =1   (2)
Ta có hệ phương trình :
\begin{cases}\frac{1}{x} +\frac{1}{y} =\frac{5}{24}\\\frac{51}{5x} +\frac{6}{5y} =1 \end{cases} (*)
Đặt : u = 1/x ; v = 1/y. ta được : (*)
\Leftrightarrow\begin{cases}u+v=\frac{5}{24}\\ 51u+6v=5\end{cases}\\ \Leftrightarrow\begin{cases} 24u+24v=5\\ 204u+24v=20\end{cases}\\ \Leftrightarrow\begin{cases} 24u+24v=5\\ u=\frac{1}{12}\end{cases}\\ \Leftrightarrow\begin{cases}v=\frac{1}{8} \\ u=\frac{1}{12}\end{cases}
Ta lại có : v = 1/y = 1/8 => y =8 (giờ)
Vậy : vòi 2 chảy một mình đầy bể trong 8 (giờ).

===============================

BÀI TẬP BỔ SUNG :

BÀI 1 : viết phương trình tđường thẳng đi qua hai điểm  A(1, -2) và B (-1, 3)

Giải.

Gọi đường thẳng (d) : y = ax + b
A(1, -2) 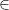\in   (d) : y = ax + b
=> a + b = -2 (1)
B (-1, 4) 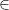\in   (d) : y = ax + b
=> -a + b = 4 (2)
Từ (1) và (2), ta có hệ phương trình :
\begin{cases}a+b=-2(1) \\ -a+b=4 (2)\end{cases}\\ \Leftrightarrow\begin{cases}a=-3\\ b=1 \end{cases}
Vậy : đường thẳng (d) : y = -3x + 1.