Bài 2
Hình thang
–o0o–
1. Định nghĩa :
Hình thang là tứ giác có hai cạnh đối song song.
DC : cạnh đáy lớn.
AD, BC : cạnh bên.
AH : đường cao.
2. Hình thang vuông :
Hình thang vuông là Hình thang có một góc vuông.
BÀI TẬP SGK
Bài 8 trang 71 SGK :
hình thang ABCD (AB // CD) có  và
và  . Tính các góc của hình thang.
. Tính các góc của hình thang.
Giải.
Ta được :
suy ra : 
Ta được :
Suy ra : 
BÀI 9 /T71: cho tứ giác ABCD có BC = BA, AC là tia phân giác góc A. Chứng minh ABCD là hình thang.
giải.
Xét tam giác ABC ta có :
BC = BA (gt)
= > tam giác ABC cân tại B.
= > 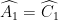
Mà :  (AC là tia phân giác góc BAD)
(AC là tia phân giác góc BAD)
= > 
= > BC // AD (hai goc C và A ở vị trí sole trong)
= > ABCD là hình thang.



