Bài 3
HÌNH THANG CÂN
–o0o–
1. Định nghĩa :
Tứ giác ABCD Hình thang cân ta có :
- AB // DC
- góc D = góc C hoặc góc A = góc B
2. Tính chất :
Định lí 1 :
Trong Hình thang cân, hai cạnh bên bằng nhau.
Tứ giác ABCD (AB // DC) Hình thang cân ta có :
hai cạnh bên :AD = BC.
Định lí 2 :
Trong Hình thang cân, hai đường chéo bằng nhau.
hai đường chéo : AC = BD.
3. Dấu hiệu nhận biết :
- Hình thang có hai góc kề một cạnh đấy bằng nhau là Hình thang cân.
Hình thang hai đường chéo bằng nhau là Hình thang cân.
BÀI TẬP SGK
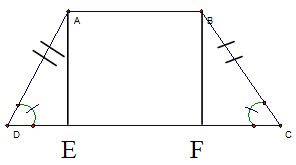
BÀI 12 /T74 : Cho Hình thang cân ABCD (AB // DC, AB < DC). Kẻ các đường cao AE, BF. chứng minh rằng : DE = CF.
Xét Δ AED và Δ BFC ta có :
AD = BC (cmt)
= > Δ AED = Δ BFC (cạnh huyền – góc nhọn)
= > DE = CF
BÀI 13 TRANG 74 : Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Giải.
Chứng minh : EC = ED và AE = EB
AD = BC; AC = BD
Xét ΔADC và ΔBDC ta có :
DC cạnh chung.
AD = BC; AC = BD (cmt)
=> ΔADC = ΔBDC (c -c -c)
=>  (góc tương ứng)
(góc tương ứng)
=> ΔDEC cân tại E
=> EC = ED đpcm
Cmtt ta được : EA = EB.
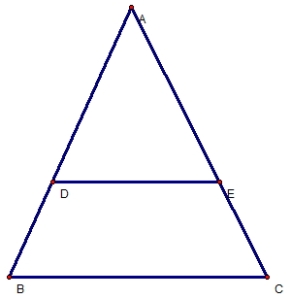
BÀI 15 TRANG 74 :
a) cm : BDEC là hình thang cân.
ΔABC cân tại A, suy ra :
AD = AE (gt)
=> ΔADE cân tại A
=>  (2)
(2)
Từ (1), (2) suy ra : 
=> DE // BC ( ở vị trí đồng vị)
ở vị trí đồng vị)
=> BDEC là hình thang
Mà :  (cmt)
(cmt)
=> BDEC là hình thang cân.
b) Tính các góc của hình thang cân BDEC :
Ta có :