Blog Toán Học

BÀI 3 :

Liên hệ giữa DÂY và KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY

–o0o–

Định lí 1 :

Trong một đường tròn :

Hai dây bằng nhau thì cách đều tâm.

Hai dây cách đều tâm thì bằng nhau.

Định lí 2 :

Trong hai dây của một đường tròn :

Dây nào lớn hơn thì dây đó gần tâm hơn .

Dây nào gần tâm hơn thì dây đó lớn hơn .

================================================

BÀI TẬP SGK :

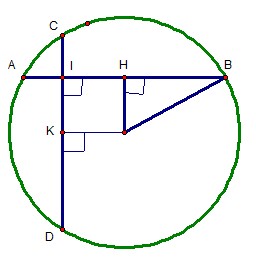
BÀI 12 TRANG 206 :

Kẻ OH vuông góc AB tại H, OK vuông góc CD tại K.

a) Tính OH :

OH vuông góc AB tại H = > HA = HA = AB/2 = 8/2 = 4cm.

Xét Δ OHB vuông tại H, theo Định lí Pitago :

OB² = OH² + HB²

= > OH²= OB² – HB² = 52 – 42 = 9

= > OH = 3cm.

b) Chứng minh : CD = AB.

Ta có :

AI = 1cm, AH = 4cm = > I nằm giữa AH

= > AH = AI + IH = > IH = 3cm.

= > IH = OH = 3cm.

Xét tứ giác OHIK ta có :

$\widehat{H}= \widehat{I}= \widehat{K}=90^0$ (gt)

= > tứ giác OHIK là hình chữ nhật

Mà : IH = OH ( cmt)

= > tứ giác OHIK là hình vuông.

= > OH = OK

= > AB = CD

—————————————————————————————————————

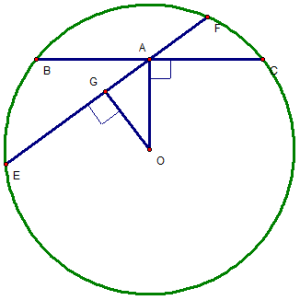
BÀI 13 TRANG 106 :

a) EH = EK

HA = HB = AB/2 (gt) = > OH $\perp$ AB

KC = KD (gt) = CD/2 = > OK $\perp$ CD

AB = CD = > OH = OK; AH = KC

Xét ΔEOH và tam giác ΔEOK, ta có :

$\widehat{H}= \widehat{K}=90^0$

EO chung.

OH = OK(cmt)

= > ΔEOH = ΔEOK

= > EH = EK

b)EA = EC :

ta có : EH = EK (cmt)

AH = KC (cmt)

= > EH + AH = EK + KC

< => EA = EC đpcm.

—————————————————————————————————————

BÀI 16 TRANG 106 :

Kẽ OG $\bot$ EF tại G.

Xét 𝛥 OAG vuông tại G, ta có :

OA > OG ( OA là cạnh huyền, OG là cạnh góc vuông)

=> AB < EF.