bài 4

một số hệ thức về cạnh và góc trong tam giác vuông

Trong tam giác vuông, mỗi cạnh góc vuông bằng :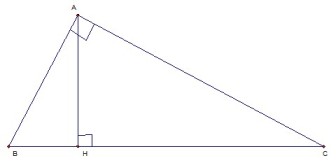

a) Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.

b) Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.

AC = BC.sin B = BC.cos C = AB.tg B = AB.cotg C.

AB = BC.sin C = BC.cos B = AC. Tam giác C = AC.cotg B

Yêu cầu :

Tìm các cạnh và các góc của tam giác vuông khi cho biết hai yếu tố.

BÀI 27 TRANG 88 :

a) Cho b = AC = 10cm; $\widehat{C}=30^0$

b) Cho c = AB = 10cm; $\widehat{C}=45^0$

c) Cho a = BC = 20cm; $\widehat{B}=35^0$

d) Cho c = AB = 21cm; b = AC = 18cm

Giải.

a) Cho b = AC = 10cm; $\widehat{C}=30^0$

Nhận xét :

cạnh góc vuông AC kề với góc C.

giải.

xét tam giác ABC vuông tại A, ta có :

$\widehat{B}+\widehat{C}=90^0$ (tổng hai góc nhọn trong tam giác vuông)

= > $\widehat{B}=90^0-\widehat{C}=90^0-30^0=60^0$

Cạnh góc vuông AB = AC.tgC = 10.tg30⁰ = 10. 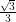$\frac{\sqrt{3}}{3}$ cm

Cạnh huyền : AC = BC.cosC

= > BC = AC/cos30⁰ = 20.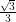 $\frac{\sqrt{3}}{3}$ cm

d) Cho c = AB = 21cm; b = AC = 18cm

Nhận xét :

Biết hai cạnh góc vuông.

xét tam giác ABC vuông tại A, theo định lí pitago :

BC² = AB²+ AC² = 21²+ 18² = 765

= > BC = $\sqrt{765}= 27,66$ cm

tgB = $\frac{AC}{AB}=\frac{18}{21}= 0,857$

= > $\widehat{B}=41^0$

$\widehat{B}+\widehat{C}=90^0$ (tổng hai góc nhọn trong tam giác vuông)

= > $\widehat{C}=90^0-\widehat{B}=90^0-41^0=49^0$