Bài 5 :

Trường hợp bằng nhau thứ ba của tam giác GÓC – CẠNH– GÓC (g – c – g)

–o0o–
Tính chất :
Nếu một cạnh và hai góc kề của tam giác này bằng với một cạnh và hai góc kề của tam giác kia thì hai tam giác bằng nhau.

Nếu ΔABC và ΔMNK, có :
  • \widehat{BAC} =\widehat{NMK}
  • AC = MK
  • \widehat{ACB} =\widehat{MKN}
ThìΔABC = ΔMNK (g – c – g)
Hệ quả 1 :
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng với một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông bằng nhau.
Hệ quả 2 :
Nếu một cạnh huyền và một góc nhọn của tam giác vuông này bằng với một cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông bằng nhau.

==============

BÀI TẬP SGK :

BÀI TẬP 35 TRANG 123 :
a)      Cmr : OA  = OB
XÉT ΔOHA và ΔOHB, có :
\widehat{OHA} =\widehat{OHB}=90^0  (gt)
OH cạnh chung.
\widehat{AOH} =\widehat{BOH}
=> ΔOHA và ΔOHB (cạnh bên – góc nhọn)
=> OA = OB
b)      CA = CB và \widehat{OAC} =\widehat{OBC}
XÉT ΔOCA và ΔOCB, có :
OA = OB (cmt)
\widehat{COA} =\widehat{COB} (At là phân giác góc xAy)
OC cạnh chung.
=> ΔOCA = ΔOCB
=> CA = CB (cạnh tương ứng) và \widehat{OAC} =\widehat{OBC}  (góc tương ứng).
———————————————————————————————————–
BÀI 41 TRANG 124 :
Chứng minh : ID = IE = IF :
Xét 𝛥 DBI và 𝛥 EBI, ta có :
\widehat{D} =\widehat{E} =90^0 (gt)
IB cạnh chung.
\widehat{DBI} =\widehat{IBE}  (IB là tia phân giác góc ABC)
=> 𝛥 DBI = 𝛥 EBI (cạnh huyền – góc nhọn)
=> ID = IE.
cmtt, ta được :  IE = IF
=> ID = IE = IF.

===============================

BÀI TẬP MỞ RỘNG :

Bài 1 : Cho tam giác ABC. Gọi D là trung điểm AC. Từ A vẽ đường thẳng song song BC cắt BD tại E. trên cạnh BC lấy M, đường thẳng DM cắt AE tại N  Chứng minh :
  1. AE = BC.
  2. D là trung điểm MN.
  3.  AB // EC
GIẢI.
 hai tam giac bang nhau GOC - CANH - GOC
1. AE = BC :
Xét ΔADE và ΔCDB, ta có :
\widehat{A_1}=\widehat{C_1}  (so le trong).
DA = DC (D là trung điểm AC)
\widehat{ADE}=\widehat{CDB}  (đối đỉnh).
=> ΔADE = ΔCDB (g – c – g)
=> AE = BC.
2 D là trung điểm MN : 
Xét ΔNDE và ΔMDB, ta có :
\widehat{E_1}=\widehat{B_1}  (so le trong).
DE = DB (ΔADE = ΔCDB)
\widehat{EDE}=\widehat{MDB}  (đối đỉnh).
=> ΔADE = ΔCDB (g – c – g)
=> DM = DN
Hay D là trung điểm MN.
3.AB // EC :
Xét ΔADB và ΔCDE, ta có :
DA = DC (D là trung điểm AC)
\widehat{ADB}=\widehat{CDE}  (đối đỉnh).
DE = DB (ΔADE = ΔCDB)
=> ΔADE = ΔCDB (c – g – c)
=> \widehat{BAD}=\widehat{DCE}
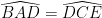
Mà : 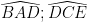\widehat{BAD};\widehat{DCE}  ở vị trí so le trong.
=> AB // EC.

===============================

BÀI TẬP RÈN LUYỆN :

BÀI 1 :
Cho tam giác ABC, gọi D là trung điểm của BC. trên tia đối của tia DA lấy điểm E sao cho DE = DA. Chứng minh rằng :
  1. ΔACD = ΔEBD.
  2. AC // BE.
  3. AB = CE.
BÀI 2 :
Cho tam giác ABC vuông tại A, lấy M  là trung điểm của BC. trên tia DA lấy điểm D sao cho AM = MD. Chứng minh :
  1. ΔAMB = ΔDMC.
  2. AB // CD.
  3. CDA vuông.
  4. AM = BM.