Trường hợp bằng nhau thứ hai của hai tam giác CẠNH – GÓC – CẠNH (C – G – C)
–o0o–
1.Tính chất :
Nếu hai cạnh và góc xen giữa của tam giác này bằng với hai cạnh và góc xen giữa của tam giác kia thì hai tam giác bằng nhau.
Nếu ΔABC và ΔMNK, có :
- AB = MN
- AC = MK
Thì ΔABC = ΔMNK (c – g – c)
2. Hệ quả :
Nếu hai cạnh góc vuông của tam giác vuông này bằng với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông bằng nhau.
=================
BÀI TẬP SGK:
AB = AD ( gt)
BE = DC (gt)
=> AB + BE = AD + DC
Hay AE = AC
Xét ΔABC và ΔADE, ta có :
AB = AD ( gt)
AC = AE (cmt).
=> ΔABC = ΔADE (C -G -C)
=============================================
BÀI TẬP mở rộng :
BÀI 1 : Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm N sao cho MN = MA. chứng minh : c) AC = BN. b) AB // NC
giải.
MB = MC (M là trung điểm của BC)
MA = MN (gt).
=> ΔACM = ΔNBM (c -g -c) => AC = BN
b) BC vuông góc DE : Xét ΔABM và ΔNCM, ta có :
MB = MC (M là trung điểm của BC)
MA = MN (gt).
=> ΔABM = ΔNCM (c -g -c)
=>
Mà : 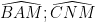 ở vị trí so le trong. => AB // NC.
ở vị trí so le trong. => AB // NC.
———————————————————
BÀI 2 : Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại D Trên cạnh BC lấy điểm E sao cho BE = AB.chứng minh : BC vuông góc DE.
Giải.
BE = AB (gt)
BD cạnh chung.
=> ΔABD = ΔEBD (c -g -c)
=>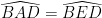
Mà : 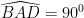 (gt)
(gt)
=>  Hay BC vuông góc DE.
Hay BC vuông góc DE.
—————————————
BÀI 3 : Cho tam giác ABC . gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.
GIẢI.
Xét ΔBCD và ΔBMD, ta có :
DB = DA (D là trung điểm của AB)
DC = DM (gt).
=> ΔBCD = ΔBMD (c -g -c)
=>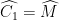 và BC = AM.
và BC = AM.
Mà :  ở vị trí so le trong. => BC // AM.
ở vị trí so le trong. => BC // AM.
Cmtt, ta được : BC // AN và BC = AN.
ta có : BC // AM (cmt) và BC // AN (cmt)
=> A, M. N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) và (2), suy ra : A là trung điểm của MN.





