Bài 3 :
Trường hợp bằng nhau thứ nhất của tam giác CẠNH – CẠNH – CẠNH (C – C – C)
–o0o–
VẼ TAM GIÁC CÓ ĐỘ DÀI BA CẠNH :
BÀI 15 TRANG 114 :
vẽ tam giác NMP biết MN = 2,5cm; NP = 3cm; PM = 5cm.
Giải.
- Vẽ đoạn PM = 5cm.
- Vẽ đường tròn (P) tâm P bán kính PN = 3cm.
- Vẽ đường tròn (M) tâm M bán kính MN = 2,5cm.
- Đường tròn (P) cắt đường tròn (M) tại N.
- Vẽ đoạn PN và MN, ta được tam giác NMP.
HAI TAM GIÁC BẰNG NHAU CÓ BA CẠNH TƯƠNG ỨNG BẰNG NHAU :
1. Tính chất :
Nếu ba cạnh của tam giác này bằng với ba cạnh của tam giác kia thì hai tam giác bằng nhau.
Nếu ΔABC và ΔMNK, có :
- AB = MN
- BC = NK
- AC = MK
Thì ΔABC = ΔMNK
=======================
BÀI TẬP SGK:
Chứng minh rằng :
a) ΔADE = ΔBDE
b) 
GIẢI.
Xét ΔADE và ΔBDE , có :
DA = AB (gt)
EA = EB (gt)
DE cạnh chung.a)
=> ΔADE = ΔBDE (c – c – c)
b) => (góc tương ứng)
(góc tương ứng)
—————————————
BÀI 32 SBT TRANG 141 :
Cho tam giác ABC có AB =AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc BC.
Giải.
AB =AC (gt)
MB = MC (M là trung điểm của BC)
AM cạnh chung
=> ΔAMB = ΔAMC (c – c – c)
=> 
Mà :  (hai góc kề bù)
(hai góc kề bù)
=> 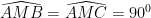
Hay AM  BC.
BC.
=============================================
BÀI TẬP RÈN LUYỆN :
BÀI 1 :
Cho tam giác ABC có AB =AC. Gọi M là trung điểm của BC. chứng minh :
a) AM là đường trung trực của BC.
b) kẽ đường phân giác Ax của góc ngoài A. chứng minh : Ax // BC




