Bài 7

TỨ GIÁC NỘI TIẾP.

–o0–

Định nghĩa :

Một tứ giác có bốn đỉnh nằm trên đường tròn được gọi là tứ giác nội tiếp.

Định lí :

Trong một tứ giác nội tiếp, tổng số đo hai góc đối bằng 180⁰.

Định lí đảo :

Trong một tứ giác tổng số đo hai góc đối bằng 180⁰ thì tứ giác đó nội tiếp được trong một đường tròn.

Dấu hiệu một tứ giác nội tiếp trong đường tròn :

Tứ giác có tổng số đo hai góc đối bằng 180⁰
Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
Tứ giác có bốn đỉnh cách đều một điểm.
Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.

===============================================

BÀI TẬP SGK – SBT

BÀI 58 TRANG 90 :

Ta có :

$\widehat{ABC} =\widehat{ACB} =60^0$ (∆ABC đều)

$\widehat{DCB} =\widehat{ACB}:2 =30^0$ (gt)

Ta có : $\widehat{ACD} =\widehat{ACB}+\widehat{DCB} =90^0$ (1)

Xét ∆DBC, ta có :

DB = DC (gt)

=> ∆DBC cân tại D.

=> $\widehat{DCB} =\widehat{DBC} =30^0$

Ta có : $\widehat{ABD} =\widehat{ABC}+\widehat{DBC} =90^0$ (2)

Từ (1) và (2), ta được :

$\widehat{ABD} +\widehat{ACD} =90^0+90^0=180^0$

=> tứ giác ABDC nội tiếp (O) (tổng hai góc đối 180⁰)

Mà : $\widehat{ABD}=90^0$ (cmt)

=> AD là đường kính của (O).

=> tâm O là trung điểm AD.

——————————————————————————————-

BÀI 58 TRANG 90 :

Xét ∆ADP , ta có :

$\widehat{ABC} +\widehat{APC} =180^0$ (tứ giác ABCP nội tiếp)

Mà : $\widehat{APD} +\widehat{APC} =180^0$ ( D, P, C thẳng hàng)

=> $\widehat{APD} =\widehat{ABC}$

Mặt khác : $\widehat{ADP} =\widehat{ABC}$ ( ABCD là hình bình hành)

=> $\widehat{APD} =\widehat{ADP}$

=> ∆ADP cân tại A.

=> AD = AP.

——————————————————————————————

BÀI 60 TRANG 90 :

$\widehat{TSR} =\widehat{IAP}$ (tứ giác ATSI nội tiếp (O3))

$\widehat{IBQ} =\widehat{IAP}$ (tứ giác APBI nội tiếp (O2))

$\widehat{IBQ} =\widehat{QRS}$ (tứ giác BQRI nội tiếp (O1))

=> $\widehat{TRS} =\widehat{QRS}$

Mà : $\widehat{TRS} ,\widehat{QRS}$ ở vị trí so le trong.

=> QR // ST

==============================

BÀI TẬP BỔ SUNG :

BÀI 1 :

Cho ∆ABC vuông tại A. M thuộc AC. Đường tròn (O) đường kính MC cắt BM tại D và cắt AD tại S. chứng minh rằng :

ABCD là tứ giác nội tiếp.
CA là tia phân giác của $\widehat{SBC}$

GIẢI.

ABCD là tứ giác nội tiếp :

Ta có :

$\widehat{MDC}=90^0$ (góc nội tiếp chắn ½ (O))

=> $\widehat{BAC} =\widehat{BDC}=90^0$

=> ABCD là tứ giác nội tiếp (I) (hai góc cùng nhìn BC dưới goc vuông)

CA là tia phân giác của $\widehat{SBC}$

Ta có : $\widehat{ACB} =\widehat{ADB}$ (gnt cùng chắn cung AB của (I))

$\widehat{ACS} =\widehat{ADB}$ (MDSC là tứ giác nội tiếp (O))

=> $\widehat{ACB} =\widehat{ACS}$

=> CA là tia phân giác của $\widehat{SBC}$

—————————————————————————————————————–

BÀI 2 :

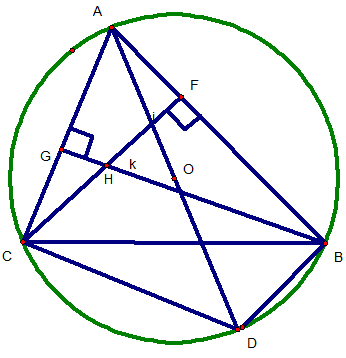
Cho tam giác ABC nội tiếp đường tròn (O) đường kính AD. H là trực tâm tam giác ABC. Kẻ đường hính OI vuông góc BC tại I. Chứng minh :

BHCD là hình bình hành.
I, H, D thẳng hàng.
AH = 2OI

GIẢI

BHCD là hình bình hành :

$\widehat{ACD}=90^0$ (góc nội tiếp chắn ½ (O))

=> CD $\bot$ AC

Mà : BH $\bot$ AC (H là trực tâm)

=> CD // BH (cùng vuông góc AC)

Cmtt, ta được : BD // CH

Xét tứ giác BHCD , ta có :

BHCD là hình bình hành

CD // BH (cmt)

BD // CH (cmt)

tứ giác BHCD là hình bình hành.

b)I, H, D thẳng hàng.

đường kính OI $\bot$ BC tại I

=> IB = IC

Mà : hai đường chéo HD và BC của hình bình hành BHCD cắt nhau tại trung điểm mỗi đường.

=> IH = ID

Hay I, H, D thẳng hàng.

3. AH = 2OI

Xét 𝛥 ABC có H là trực tâm

=> AH $\bot$ BC

Mà : OI $\bot$ BC

=> OI // AH

Xét 𝛥 AHD, ta có :

OA = OD (AD là đường kính của (O))

OI // AH (cmt)

=> OI là đường trung bình trong 𝛥 AHD

=> AH = 2OI