Blog Toán Học

PHÂN THỨC ĐẠI SỐ : tính chất – rút gọn – quy đồng phân thức đại số.

–o0o–

phân thức đại số có dạng 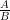$\frac{A}{B}$ . Trong đó A, B là đa thức đại số và B ≠ 0. Ta gọi :

Hai phân thức bằng nhau :

$\frac{A}{B}=\frac{C}{D}$ nếu A.D = C.B

Tính nhân :

Nếu nhân tử và mẫu của một phân thức với cùng một đa thức khác 0 thì được một phân thức bằng phân thức đã cho :

$\frac{A}{B}=\frac{A.M}{B.M}$ (M là một đa thức khác 0).

Tính chia :

Nếu chia tử và mẫu của một phân thức với cùng một nhân tử chung thì được một phân thức bằng phân thức đã cho :

$\frac{A}{B}=\frac{A:N}{B:N}$ (N là một nhân tử chung).

Một số qui tắc đổi dấu :

Phương pháp : dùng tính chất chia :

Phân tích tử và mẫu của một phân thức (nếu cần) thành nhân tử. tìm nhân tử chung.
Chia tử và mẫu của một phân thức với cùng một nhân tử chung.

Ví dụ minh họa :

Rút gọn phân thức : $\frac{x^3-2x^2y+xy^2}{x^2y-xy^2}$

Ta có :

x³ – 2x²y + xy² = x(x² – 2xy + y² )=x(x – y)²

x²y – xy² = xy(x – y)

ta được : $\frac{x^3 -2x^2y+xy^2}{x^2y-xy^2}=\frac{x(x-y)^2}{xy(x-y)}=\frac{x-y}{y}$

Phương pháp : dùng tính chất nhân :

Phân tích tử và mẫu của một phân thức (nếu cần) thành nhân tử. tìm mẫu thức chung.
Tìm nhân tử phụ của mỗi mẫu thức.
nhân tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Ví dụ minh họa : bài 15a trang 43 :

Quy đồng mẫu thức của phân thức : $\frac{5}{2x+6}$ và $\frac{3}{x^2-9}$

Ta có :

2x + 6 = 2(x + 3)

x² – 9 = (x – 3)(x + 3)

MTC : 2(x – 3)(x + 3)

Nhân tử phụ của mẫu 2x + 6 là : [2(x – 3)(x + 3)] : [2(x + 3)] = x – 3

Nhân tử phụ của mẫu x² – 9 là : [2(x – 3)(x + 3)] : [(x – 3)(x + 3)] = 2

Quy đồng :

$\frac{5}{2x+6}=\frac{5(x-3)}{(2x+6)(x-3)}= \frac{5(x-3)}{2(x+3)(x-3)}$

$\frac{3.2}{(x^2-9).2}=\frac{6}{2(x+3)(x-3)}$