Bài 2

Định lí Talet đảo – các hệ quả.

–o0o–

I.1.    Định lí Talet đảo :
Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Hệ quả :
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại của tam giác thì nó tạo ra tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
=====================
Ví dụ : Cho tam giác ABC có AB = 28cm, AC = 20cm. trên AB lấy điểm M sao cho AM = 7cm, trên AC lấy điểm N sao cho AN = 5cm. Chứng minh MN // BC.

GIẢI.


———————————————

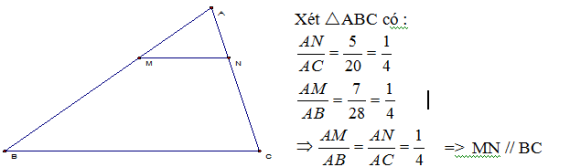
Bài 6 trang 62 :
Hình 13 a)
MN // AB vì :
Trong tam giác ABC :
AM / MC = 5/15 = 1/3
NB / NC = 7/21= 1/3
=> AM / MC = NB / NC = 1/3
=> MN // AB (định lý đảo talet)
Hình 13 b)
AB // A’B’ // A”B” vì :
Trong tam giác ABO :
OA’ / A’A = 2/3
OB’ / B’B = 3/4.5 = 2/3
OA’ / A’A = OB’ / B’B = 2/3
=> AB // A’B'(định lý đảo talet) (1)
ta lại có :
góc A = góc A’ (gt)
=> A’B’ // A”B” (2 góc ở vị trí so le trong )(2)
Từ (1) và (2), ta được : AB // A’B’ // A”B”
Bài 7 trang 62 :
Trong tam giác DEF, ta có :
MN // EF (gt)
=> EF / MN = AD / DM (hệ quả)
Hay x/8 = (9.5 + 28)/9.5
x = …
Bài 9 trang 63:
cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5cm BD = 4,5cm. tính tỉ số các khoảng cách từ D và B đến AC.
ta có :
DE vuông góc  AC (gt)
BF vuông góc AC (gt)
=> DE // BF
=> DE / BF = AD / AB = 13.5 / (13.5  + 4.5) = 3/4
Bài 10 trang 63:
xét tam giác ABH, có :
d // BH (gt)
=> AH’/AH = AB’/AB (1)
xét tam giác ABC, có :
d // BC (gt)
=> B’C’/BC = AB’/AB (2)
từ (1) và (2) , ta được : AH’/AH = B’C’/BC = AB’/AB
bài 11 trang 63 :
Cho tam giác ABC có BC = 15cm. Trên đường cao AH lấy điểm I, K sao cho AK = KI = IH. Qua I và K vẽ EF và MN song song BC.
a.    Tính MN và EF.
b.    Tính diện tích tứ giác MNFE, biết  diện tích tam giác ABC là 270cm2.