Bài 4
phương trình tích
–o0o–
Cách giải :
phương trình tích : A(x).B(x) = 0 ⇔ A(x) = 0 hoặc B(x) = 0
=================================
BÀI TẬP SGK :
BÀI 21 TRANG 17 : giải phương trình :
a) (3x – 2)(4x + 5) = 0
⇔ (3x – 2) = 0 hoặc (4x + 5) = 0
⇔ x = hoặc x =
hoặc x =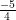
Vậy : S = {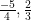 }
}
c) (4x + 2)( x2 + 1) = 0
⇔ (4x + 2) = 0 hoặc ( x2 + 1) = 0
⇔ x =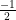 hoặc x2 = -1 (vô lí)
hoặc x2 = -1 (vô lí)
Vậy : S = {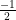 }
}
d) (2x +7)(x – 5)(5x +1) = 0
⇔ (2x +7) = 0 hoặc (x – 5) = 0 hoặc (5x +1) = 0
⇔ x =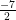 hoặc x = 5 hoặc x =
hoặc x = 5 hoặc x =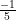
Vậy : S = {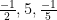 }
}
————————————————————————————–
BÀI 22 TRANG 17 : giải phương trình :
a) 2x(x – 3) +5(x – 3) = 0
⇔ (x – 3) (2x +5) = 0
⇔ (x – 3) = 0 hoặc (2x +5) = 0
⇔ x = 3 hoặc x =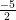
Vậy : S = {3, 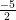 }
}
f)x2 – x – (3x – 3) = 0
⇔ x(x -1) -3(x – 1) = 0
⇔ (x – 3)(x -1) = 0
⇔ (x – 3) = 0 hoặc (x -1) = 0
⇔ x = 3 hoặc x = 1
Vậy S = {3, 1}
