BÀI 4

Vị trí tương đối của đường thẳng và đường tròn

–o0o–

Ba vị trí tương đối của đường thẳng và đường tròn :

Cho đường tròn tâm O, bán kính R. OH là khoảng cánh từ tâm đến dây đường thẳng AB.
Nếu OH < R thì : đường thẳng AB cắt  (O) tại hai điểm A và B.
Nếu OH > R thì : đường thẳng AB không cắt  (O).
Nếu OH = R thì : đường thẳng AB tiếp xúc (O) tại một điểm C.
    • đường thẳng AB gọi là tiếp tuyến.
    • điểm C gọi là tiếp điểm.
    Định lí :
    đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
    Bài 5 + 6

    Dấu hiệu và tính chất của tiếp tuyến

    –o0o–

    Dấu hiệu nhận biết tiếp tuyến của đường tròn :

    Định lí : Dấu hiệu nhận biết tiếp tuyến của đường tròn

    Nếu một đường thẳng đi qua một điểm thuộc đường tròn và vuông góc bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
    M thuộc (O) và AB vuông góc OM tại M.
    = > AB là tiếp tuyến của (O).
    Định lí : hai tiếp tuyến cắt nhau
    Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì :
    • Điểm đó cách đều hai tiếp điểm.
    • Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
    Ta có :
    Ax, By là hai tiếp tuyến của (O) tại A, B.
    Ax cắt By tại M
    = > MA = MB và OM là tia phân giác của góc AOB.
    ========================================

    BÀI TẬP SGK

    BÀI 21 TRANG 111 :
    Cho tam giác ABC có AB = 3, AC = 4 BC = 5. Vẽ đường tròn (B, BA). Chứng minh rằng AC là tiếp tuyến của đường tròn (B).
     GIẢI.
    Xét tam giác ABC có :
    BC2 = 52 = 25
    AB2 + AC2 = 32 + 42 = 25
    = > BC2 = AB2 + AC2
    = > tam giác ABC vuông tại A.
    = > AC\perpAB tại A.
    Mà : A thuộc (B, BA)
    Suy ra : AC là tiếp tuyến của (B, BA).
    BÀI 24 TRANG 111 :
    Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường thẳng vuông góc với AB, cắt tiếp tuyến tại A của đường tròn (O) tại C.
    a)      Chứng minh rằng CB là tiếp tuyến của đường tròn.
    b)      Cho bán kính đường tròn bằng 15cm, AB = 24cm. tính OC.
    Giải.
    a) CB là tiếp tuyến của đường tròn.
    Ta có : đường kính OC \perp dây AB (gt)
    = > OC đi qua trung điểm E của AB
    = > OC là đường trung trực AB.
    = > CA  = CB.
    Xét ΔOAC và ΔOBC, ta có :
    CA  = CB (cmt)
    OA = OB (bán kính)
    OC chung.
    = > ΔOAC = ΔOBC
    = > \widehat{OAC}= \widehat{OBC}
    Mà : \widehat{OAC}= 90^0
    = > \widehat{OBC}=90^0 hay OB \perp BC tại B
    Mặt khác : B thuộc (O, OB)
    Vậy : BC là tiếp tuyến của đường tròn (O).
    b)Tính OC
    ta có : AE = AB/2 = 12cm.( E trung điểm của AB)
    OA2 = OE2 + AE2 (pitago)
    = >  OE2= OA2 – AE2 = 81 = > OE = 9cm.
    Mà : OA2 = OE.OC hay 152 = 9.OC = > OC = 25cm
    BÀI 26 TRANG 115 :
    Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
    a)      Chứng minh rằng OA vuông góc BC.
    b)      Vẽ đường kính CD. Chứng minh rằng BD song song AO.
    c)      Tính độ dài các cạnh của tam giác ABC. Biết OB = 2cm, OA = 4cm.

    Giải.

    a)      Chứng minh rằng OA vuông góc BC.
    Ta có : OB = OC (bán kính)
    AB = AC (tính chất tiếp tuyến cắt nhau)
    = > OA là đường trung trực BC
    = > OA \perp BC tại E (1)
    b)Vẽ đường kính CD. Chứng minh rằng BD song song AO.
    Ta có : tam giác CDB nội tiếp (O) đường kính CD(gt)
    = > tam giác CDB vuông tại B. hay BD \perp BC (2)
    Từ (1) và  (2) suy ra : OA // DB (cùng vuông góc BC)
    c)Tính độ dài các cạnh của tam giác ABC
    ta có : OA2 = OB2 +BC2 (pitago)=>  BA2 = OA2 – OB2 = 16 – 4 = 12cm
    = > AB = 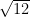\sqrt{12} = 2\sqrt{3}cm
    Mà : AC = AB = 2\sqrt{3}
    Theo hệ thức lượng : OA.EB = OB.BC <=>4.EB = 2. 2\sqrt{3}
    = > BE =  \sqrt{3}cm
    BC = 2.BE = 2\sqrt{3}cm