Bài 6+7

Phép NHÂN và phép CHIA các phân thức đại số

–o0o–

1. Phép nhân các phân thức đại số :

Quy tắc :

Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau :

$\frac{A}{B} . \frac{C}{D}= \frac{A.C}{B.D}$

2. Phân thức nghịch đảo :

Hai phân thức gọi là nghịch đảo của nhau nếu tích của chúng bằng 1.

Tổng quát :

Nếu phân thức 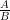$\frac{A}{B}$ khác 0 thì $\frac{A}{B} . \frac{b}{a}=1$ . Do đó :

$\frac{B}{A}$ là Phân thức nghịch đảo của Phân thức $\frac{A}{B}$

$\frac{A}{B}$ là Phân thức nghịch đảo của Phân thức $\frac{B}{A}$

3. Phép chia các phân thức đại số :

Quy tắc :

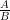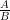Muốn chia phân thức $\frac{A}{B}$ cho phân thức $\frac{C}{D}$ khác 0. Ta nhân $\frac{A}{B}$ với Phân thức nghịch đảo của phân thức $\frac{C}{D}$

$\frac{A}{B}:\frac{C}{D}= \frac{A}{B} . \frac{D}{C}= \frac{A.D}{B.C}$

===========================

BÀI TẬP SGK :

BÀI 38 TRANG 52 : thực hiện các phép tính :

a) $\frac{15x}{7y^3} . \frac{2y^2}{x^2}= \frac{15x. 2y^2}{7y^3. x^2}=\frac{30}{7xy}$

b) $\frac{4y^2}{11x^4} . (-\frac{3x^2}{8y})=\frac{4y^2}{11x^4} . \frac{-3x^2}{8y}= \frac{ 4y^2. (-3x^2)}{11x^4. 8y }=\frac{-3y}{22x^2}$

c) $\frac{x^3-8}{5x+20} . \frac{x^2+4x}{x^2+4x+4}$

$= \frac{ (x^3-8). (x^2+4x) }{5x+20. x^2+4x+4}=\frac{(x-2)( x^2+4x+4)x(x+4)}{5(x+4)( x^2+4x+4)}=\frac{x(x-2)}{5}$

BÀI 38 TRANG 52 : thực hiện các phép tính :

a) $\frac{5x+10}{4x-8} . \frac{4-2x}{x+2}= \frac{(5x+10). (4-2x) }{(4x-8). (x+2)}$

$= \frac{(5(x+2). -2(x-2) }{4(x-2). (x+2)}=-\frac{5}{2}$

b) $\frac{x^2-36}{2x+10} . \frac{3}{6-x}= \frac{(x^2-36).3}{(2x+10). (6-x) }$

$= \frac{(x-6)(x+6).3}{2(x+5). -(x-6) }=\frac{-3(x+6)}{ 2(x+5)}$

BÀI 42 TRANG 54 : thực hiện các phép tính chia :

a) $(-\frac{20x}{3y^2}):(-\frac{4x^3}{5y})=\frac{-20x}{3y^2}:\frac{-4x^3}{5y}$
$=\frac{-20x}{3y^2}.\frac{5y}{-4x^3}=\frac{-20x . 5y }{3y^2. }{-4x^3}=\frac{25}{3x^2y}$
b) $\frac{4x+12}{(x+4)^2}:\frac{3(x+3)}{x+4}=\frac{4x+12}{(x+4)^2}.\frac{ x+4}{ 3(x+3)}$
$=\frac{4(x+3)( x+4)}{(x+4)^2.3(x+3)}=\frac{4}{3(x+4)}$