Bài 7
HÌNH BÌNH HÀNH
–o0o–
1. Định nghĩa :
hình bình hành là tứ giác có hai cặp cạnh đối song song.
2. Định lí :
Trong hình bình hành :
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết :
- Tứ giác có các cạnh đối song song là hình bình hành.
- Tứ giác có các cạnh đối bằng nhau là hình bình hành.
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có các góc đối song song là hình bình hành.
- Tứ giác có Hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
===============
BÀI TẬP SGK :
BÀI 44 TRANG 92 :
Hình bình hành ABCD, ta được :AD // BC ; AD = BC
BF = BC / 2 (F là trung điểm BC)
AD = BC (cmt)
=> ED = BF
Xét tứ giác BFDE ta có :
AD // BC (cmt)
=> BF // ED (E 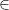 AD, F
AD, F 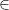 BC)
BC)
Mà : BF = ED (cmt)
=> tứ giác BFDE là Hình bình hành.
=> BE = DF
BÀI 45 TRANG 92 :
Hình bình hành ABCD, ta được :AD // BC ; 
Ta có :
=> 
Mặt khác :  (so le trong)
(so le trong)
=> DE // BF ( ở vị trí đồng vị)
ở vị trí đồng vị)
b) tứ giác DEBF là hình gì ?
xét tứ giác DEBF :
AB // DC (cmt)
=> BE // FD (E 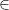 AB, F
AB, F 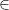 DC)
DC)
Mà : DE // BF (cmt)
=> DEBF Hình bình hành.
BÀI 47 TRANG 93 :
Cho hình 72 Hình bình hành ABCD.
a) CHỨNG MINH : AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh rằng : A, O, C thẳng hàng.
GIẢI.
Hình bình hành ABCD, ta được : AD = BC; AD // BC
Xét ΔAHD và ΔCKB, ta có :
AD = BC (cmt)
=> ΔAHD = ΔCKB (cạnh huyền – góc nhọn)
=> AH = CK
Mặt khác :
AH  BD (gt)
BD (gt)
CK  BD (gt)
BD (gt)
=> AH // CK
Xét tứ giác AHCK, ta có :
AH = CK (cmt)
AH // CK (cmt)
=> AHCK là Hình bình hành.
b) A, O, C thẳng hàng.
Ta có : AHCK là Hình bình hành => hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường.
Mà : O là trung điểm của HK (gt)
=> O cũng là trung điểm của AC
Hay A, O, C thẳng hàng.
——————————————————————————————————
Xét ΔABC, ta có :
EA = EB (gt)
FB = FC (gt)
=> EF là đường trung bình
=> EF = AC : 2 VÀ EF // AC. (1)
Cmtt, ta được : HG = AC : 2 VÀ HG // AC. (2)
Từ (1) và (2), suy ra : HG = EF và HG // EF
=> tứ giác EFGH là hình bình hành.
——————————————————————————————————
a) AI // CK
hình bình hành ABCD, suy ra :
AB = CD và AB // CD
Mà : I, K lần lược là trung điểm AB, CD
=> AK = CI và AK // CI
=>AKCI là hình bình hành
=> AI // CK
b) DM = MN = NB
Xét ΔDCN, ta có :
AI // CK hay IM // CN
IC = ID (gt)
=> MD = MN (3)
Cmtt, ta được : MN = NB (4)






