Bài 9
Tính chất ba đường cao của tam giác
–o0o–
Định nghĩa :
Trong tam giác, đoạn thẳng kẻ vuông góc từ đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao.
Định lí :
Ba đường cao của tam giác cùng đi qua một điểm. điểm này gọi là trực tâm.
Tính chất :
Trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung , đường phân giác, đường cao xuất phát từ đỉnh đối diện của cạnh đó.
=================================
BÀI TẬP SGK :
BÀI 59 TRANG 83 : Cho hình 57 :
- Chứng minh : NS
ML
- Khi
. tính
;
GIẢI.
A/ Chứng minh : NS  ML
ML
LP  MN (gt) => LP là đường cao thứ nhất.
MN (gt) => LP là đường cao thứ nhất.
MQ  LN (gt) => MQ là đường cao thứ hai.
LN (gt) => MQ là đường cao thứ hai.
LP cắt MQ tại S.
=> S là trực tâm của ΔMNL
=> NS là đường cao thứ ba.
=> NS  ML
ML
b/ tính  ;
; 
Xét tam giác MNQ, ta có :
=> 
Xét tam giác MSP, ta có :
=> 
Mà : 
=> 
———————————————————————————————————–
BÀI 78 TRANG 32 SBT :
Cho tam giác ABC cân tại A, có đường cao CH cắt tia phân giác góc A tại D. chứng minh BD vuông góc AC.
GIẢI.
AE là tia phân giác (gt)
=> AE đường cao thứ nhất.
CH đường cao thứ hai (gt) .
AE cắt CH tại D.
=> D là trực tâm.
=> BD là đường cao thứ ba.
=> BD vuông góc AC.
BÀI tổng ôn :
Cho tam giác ABC vuông tại A (AB < AC).Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.
a) Chứng minh : BC = DE.
b) Chứng minh : tam giác ABD vuông cân và BD // CE.
c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M. từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N . Chứng minh : NM // AB.
d) Chứng minh : AM = DE/2.
GIẢI.
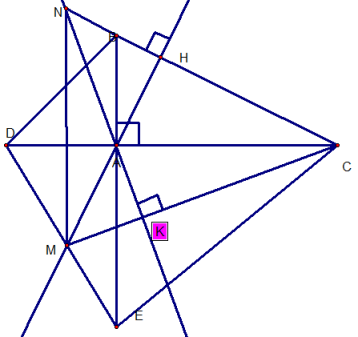
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD  AE
AE
=> 
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt : 
=> 
mà : 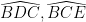 ở vị trí so le trong
ở vị trí so le trong
=> BD // CE
b) Xét Δ MNC, ta có :
NK  MC = > NK là đường cao thứ 1.
MC = > NK là đường cao thứ 1.
MH  NC = > MH là đường cao thứ 2.
NC = > MH là đường cao thứ 2.
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN  AC tại I.
AC tại I.
mà : AB  AC
AC
=> MN // AB.
c) Xét Δ AMC, ta có :
=>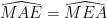 (cùng phụ góc ABC)
(cùng phụ góc ABC)
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 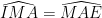 (so le trong)
(so le trong)
mà : 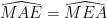 (cmt)
(cmt)
=> 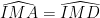
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.


