Phương pháp chứng minh 2 tam giác bằng nhau (cạnh – góc – cạnh)
BÀI 1 : Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm N sao cho MN = MA. chứng minh : c) AC = BN. b) AB // NC
giải.
a) AC = BN :
MB = MC (M là trung điểm của BC)
MA = MN (gt).
=> ΔACM = ΔNBM (c -g -c)
=> AC = BN b) BC vuông góc DE :
Xét ΔABM và ΔNCM, ta có :
MB = MC (M là trung điểm của BC)
MA = MN (gt).
=> ΔABM = ΔNCM (c -g -c)
=>
Mà : 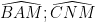 ở vị trí so le trong. => AB // NC.
ở vị trí so le trong. => AB // NC.
———————————————————
BÀI 2 : Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại D Trên cạnh BC lấy điểm E sao cho BE = AB.chứng minh : BC vuông góc DE.
Giải.
BE = AB (gt)
BD cạnh chung.
=> ΔABD = ΔEBD (c -g -c)
=>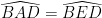
Mà : 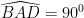 (gt)
(gt)
=>  Hay BC vuông góc DE.
Hay BC vuông góc DE.
—————————————
BÀI 3 : Cho tam giác ABC . gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.
GIẢI.
Xét ΔBCD và ΔBMD, ta có :
DB = DA (D là trung điểm của AB)
DC = DM (gt).
=> ΔBCD = ΔBMD (c -g -c)
=>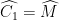 và BC = AM.
và BC = AM.
Mà :  ở vị trí so le trong. => BC // AM.
ở vị trí so le trong. => BC // AM.
Cmtt, ta được : BC // AN và BC = AN.
ta có : BC // AM (cmt) và BC // AN (cmt)
=> A, M. N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) và (2), suy ra : A là trung điểm của MN.



