Blog Toán Học

Phương pháp chứng minh 2 tam giác bằng nhau 

(góc – cạnh – góc)

Bài 1 : Cho tam giác ABC. Gọi D là trung điểm AC. Từ A vẽ đường thẳng song song BC cắt BD tại E. trên cạnh BC lấy M, đường thẳng DM cắt AE tại N  Chứng minh :

1. AE = BC.
2. D là trung điểm MN.
3.  AB // EC

GIẢI.

 

1. AE = BC :

Xét ΔADE và ΔCDB, ta có :

 (so le trong).

DA = DC (D là trung điểm AC)

 (đối đỉnh).

=> ΔADE = ΔCDB (g – c – g)

=> AE = BC.

2 D là trung điểm MN : 

Xét ΔNDE và ΔMDB, ta có :

 (so le trong).

DE = DB (ΔADE = ΔCDB)

 (đối đỉnh).

=> ΔADE = ΔCDB (g – c – g)

=> DM = DN

Hay D là trung điểm MN.

3.AB // EC :

Xét ΔADB và ΔCDE, ta có :

DA = DC (D là trung điểm AC)

 (đối đỉnh).

DE = DB (ΔADE = ΔCDB)

=> ΔADE = ΔCDB (c – g – c)

=> 

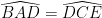
Mà : 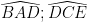 ở vị trí so le trong.

=> AB // EC.